jueves, 30 de septiembre de 2010
domingo, 12 de septiembre de 2010
Plano cartesiano y ubicación de puntos
Apreciables alumnos esta actividad tiene por objeto ver todo lo referente al sistema de coordenadas rectangulares, y su representación de puntos. Desde Historia, quien la invento, lo que opinan sobre la representación del plano cartesiano etc.
Espero tus comentarios
Atte.
Profesor. Roberto González Olivares.
El plano cartesiano está formado por dos rectas numéricas, una horizontal y otra vertical
que se cortan en un punto. La recta horizontal es llamada eje de las abscisas o de las equis
(x), y la vertical, eje de las ordenadas o de las yes, (y); el punto donde se cortan recibe el
nombre de origen.
El plano cartesiano tiene como finalidad describir la posición de puntos, los cuales se representan por sus coordenadas.
Las coordenadas se forman asociando un valor del eje de las equis (x) y uno de las yes
(y), respectivamente, esto indica que un punto se puede ubicar en el plano cartesiano con
base en sus coordenadas, lo cual se representa como: P (x, y).
Para localizar puntos en el plano cartesiano se debe llevar a cabo el siguiente procedimiento:
1. Para localizar la abscisa o valor de x, se cuentan las unidades correspondientes hacia la derecha si son positivas o hacia la izquierda si son negativas, a partir del punto de origen, en este caso el cero.
2. Para ubicar las ordenadas (eje y), desde donde se localiza el valor de x, se cuentan
las unidades correspondientes hacia arriba si son positivas o hacia abajo, si son
negativas y de esta forma se localiza cualquier punto dadas sus coordenadas.
Ejemplo de ubicación de puntos en el Plano.
Determina la ubicación en el Plano Cartesiano de los siguientes puntos:
P1(3, 2) P2(-2, -4) P3(-3, 3) P4(1, -2)
sábado, 11 de septiembre de 2010
URGENTE
La pagina de WORD PRESS http//robernov123.wordpress.com// YA NO ES ahora es esta gracias por su comprension.
jueves, 9 de septiembre de 2010
PUNTOS NOTABLES DE UN TRIANGULO
PUNTOS NOTABLES DE UN TRIANGULO
Esta asignación tiene un conjunto de actividades para ayudar a familiarizarse con el SGP y de revisar un poco de geometría del triángulo de base. Después de examinar las actividades para el en la tarea, elegir algún tema de un breve relato. El reportaje puede ser una de las pruebas, pero no tiene que ser. Podría ser algo de exploración que trataría con los estudiantes. O usted podría tomar uno de los temas (por ejemplo, las medianas) y explorar algunos de la geometría estándar para el tema.
________________________________________
1. El centro de gravedad (G) de un triángulo es la intersección común de las tres medianas. Una mediana de un triángulo es el segmento desde un vértice al punto medio del lado opuesto.
Geometer's Sketchpad Uso (SGP) para construir el centro de gravedad y su ubicación para explorar diferentes formas de triángulos.
________________________________________
2. El ortocentro (H) de un triángulo es la intersección común de las tres líneas que contienen las altitudes. Una altitud es un segmento perpendicular desde un vértice a la línea del lado opuesto. (Nota: al pie de la perpendicular puede estar en la extensión del lado del triángulo.) Debe quedar claro que H no tiene que estar en los segmentos que son las alturas. Más bien, H se encuentra en las líneas extendía a lo largo de las altitudes.
El uso del SGP para construir un ortocentro H y su ubicación para explorar diferentes formas de triángulos. (Asegúrese de que su construcción es válido para triángulos obtusos.)
________________________________________
3. El circuncentro (C) de un triángulo es el punto en el plano equidistante de los tres vértices del triángulo. Desde un punto equidistante de dos puntos se encuentra sobre la mediatriz del segmento determinado por los dos puntos, C se encuentra en la mediatriz de cada lado del triángulo. Nota: C puede estar fuera del triángulo.
Construya el circuncentro C y su ubicación para explorar diferentes formas de triángulos. Es el centro de la circunferencia circunscrita (el círculo circunscrito) del triángulo.
________________________________________
4. El incentro (I) de un triángulo es el punto en el interior del triángulo que es equidistante de los tres lados. Desde un punto interior a un ángulo que es equidistante de los dos lados del ángulo se encuentra en la bisectriz del ángulo, entonces debo estar en la bisectriz del ángulo de cada ángulo del triángulo.
El uso del SGP para encontrar una construcción del incentro I y explorar sus diversas formas localiza la de los triángulos. El incentro es el centro de la circunferencia inscrita (el círculo inscrito) del triángulo.
________________________________________
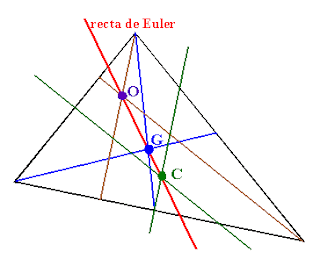
5. El uso del SGP para la construcción de G, H, C, y para el mismo triángulo. ¿Qué relaciones se pueden encontrar entre los G, H, C y I o subconjuntos de ellos? Explorar las muchas formas de triángulos.
________________________________________
6. Tome cualquier triángulo. Construir un triángulo que conecta los tres puntos medios de los lados. Esto se conoce como el triángulo medial. Es semejante al triángulo original y una cuarta parte de su área. Construir G, H, C, y para este nuevo triángulo. Compara a la G, H, C, y yo en el triángulo original.
________________________________________
7. Tome cualquier triángulo agudo. Construir un triángulo de conexión de los pies de las alturas. Esto se conoce como el triángulo órtico. Construir G, H, C, y yo por el triángulo órtico. Compara a la G, H, C, y yo en el triángulo original. ¿Puede ampliar este trabajo para los triángulos rectángulos o triángulos obtusos?
________________________________________
8. Tome una aguda triángulo ABC. Construir H y los segmentos HA, HB y HC. Construya los puntos medios de HA, HB y HC. Conectar los puntos medios para formar un triángulo. Demostrar que este triángulo es semejante al triángulo ABC y congruente con el triángulo medial. Construir G, H, C, y yo por este triángulo. Compare.
________________________________________
9. En el triángulo original misma, la construcción de los tres triángulos secundaria de los ejercicios 6, 7 y 8. Construir la circunferencia circunscrita a cada uno de los triángulos secundaria. ¿Qué se observa? ¿Puede probar su conjetura?
________________________________________
10. El círculo de los nueve puntos de cualquier triángulo pasa por los tres puntos medios de los lados, los tres pies de las alturas, y los tres puntos medios de los segmentos de los vértices respectivos ortocentro. Construir los nueve puntos, localizar el centro (N) y construir el círculo de nueve puntos.
________________________________________
11. ¿Cómo es N relacionados con G, H, C o I para los diferentes triángulos en forma?
________________________________________
12. Demuestre que las tres mediatrices de los lados de un triángulo son concurrentes.
________________________________________
13. Demostrar que las líneas de las tres alturas de un triángulo son concurrentes.
________________________________________
14. Demuestre que las tres medianas de un triángulo son concurrentes y que el punto de concurrencia, el centro de gravedad, es de dos tercios de la distancia de cada vértice al lado opuesto.
¿Cómo utilizaría SPG para ayudar a los estudiantes comprender esta relación del triángulo y sus puntos medios? ¿Cómo desarrollar un sentido de la prueba de la relación con los estudiantes?
________________________________________
15. Demuestre que las tres bisectrices de los ángulos internos de un triángulo son concurrentes.
________________________________________
16. Demostrar que cualquier bisectriz del ángulo de un triángulo es concurrente con las dos bisectrices exteriores de los ángulos opuestos de un triángulo.
Esta asignación tiene un conjunto de actividades para ayudar a familiarizarse con el SGP y de revisar un poco de geometría del triángulo de base. Después de examinar las actividades para el en la tarea, elegir algún tema de un breve relato. El reportaje puede ser una de las pruebas, pero no tiene que ser. Podría ser algo de exploración que trataría con los estudiantes. O usted podría tomar uno de los temas (por ejemplo, las medianas) y explorar algunos de la geometría estándar para el tema.
________________________________________
1. El centro de gravedad (G) de un triángulo es la intersección común de las tres medianas. Una mediana de un triángulo es el segmento desde un vértice al punto medio del lado opuesto.
Geometer's Sketchpad Uso (SGP) para construir el centro de gravedad y su ubicación para explorar diferentes formas de triángulos.
________________________________________
2. El ortocentro (H) de un triángulo es la intersección común de las tres líneas que contienen las altitudes. Una altitud es un segmento perpendicular desde un vértice a la línea del lado opuesto. (Nota: al pie de la perpendicular puede estar en la extensión del lado del triángulo.) Debe quedar claro que H no tiene que estar en los segmentos que son las alturas. Más bien, H se encuentra en las líneas extendía a lo largo de las altitudes.
El uso del SGP para construir un ortocentro H y su ubicación para explorar diferentes formas de triángulos. (Asegúrese de que su construcción es válido para triángulos obtusos.)
________________________________________
3. El circuncentro (C) de un triángulo es el punto en el plano equidistante de los tres vértices del triángulo. Desde un punto equidistante de dos puntos se encuentra sobre la mediatriz del segmento determinado por los dos puntos, C se encuentra en la mediatriz de cada lado del triángulo. Nota: C puede estar fuera del triángulo.
Construya el circuncentro C y su ubicación para explorar diferentes formas de triángulos. Es el centro de la circunferencia circunscrita (el círculo circunscrito) del triángulo.
________________________________________
4. El incentro (I) de un triángulo es el punto en el interior del triángulo que es equidistante de los tres lados. Desde un punto interior a un ángulo que es equidistante de los dos lados del ángulo se encuentra en la bisectriz del ángulo, entonces debo estar en la bisectriz del ángulo de cada ángulo del triángulo.
El uso del SGP para encontrar una construcción del incentro I y explorar sus diversas formas localiza la de los triángulos. El incentro es el centro de la circunferencia inscrita (el círculo inscrito) del triángulo.
________________________________________
5. El uso del SGP para la construcción de G, H, C, y para el mismo triángulo. ¿Qué relaciones se pueden encontrar entre los G, H, C y I o subconjuntos de ellos? Explorar las muchas formas de triángulos.
________________________________________
6. Tome cualquier triángulo. Construir un triángulo que conecta los tres puntos medios de los lados. Esto se conoce como el triángulo medial. Es semejante al triángulo original y una cuarta parte de su área. Construir G, H, C, y para este nuevo triángulo. Compara a la G, H, C, y yo en el triángulo original.
________________________________________
7. Tome cualquier triángulo agudo. Construir un triángulo de conexión de los pies de las alturas. Esto se conoce como el triángulo órtico. Construir G, H, C, y yo por el triángulo órtico. Compara a la G, H, C, y yo en el triángulo original. ¿Puede ampliar este trabajo para los triángulos rectángulos o triángulos obtusos?
________________________________________
8. Tome una aguda triángulo ABC. Construir H y los segmentos HA, HB y HC. Construya los puntos medios de HA, HB y HC. Conectar los puntos medios para formar un triángulo. Demostrar que este triángulo es semejante al triángulo ABC y congruente con el triángulo medial. Construir G, H, C, y yo por este triángulo. Compare.
________________________________________
9. En el triángulo original misma, la construcción de los tres triángulos secundaria de los ejercicios 6, 7 y 8. Construir la circunferencia circunscrita a cada uno de los triángulos secundaria. ¿Qué se observa? ¿Puede probar su conjetura?
________________________________________
10. El círculo de los nueve puntos de cualquier triángulo pasa por los tres puntos medios de los lados, los tres pies de las alturas, y los tres puntos medios de los segmentos de los vértices respectivos ortocentro. Construir los nueve puntos, localizar el centro (N) y construir el círculo de nueve puntos.
________________________________________
11. ¿Cómo es N relacionados con G, H, C o I para los diferentes triángulos en forma?
________________________________________
12. Demuestre que las tres mediatrices de los lados de un triángulo son concurrentes.
________________________________________
13. Demostrar que las líneas de las tres alturas de un triángulo son concurrentes.
________________________________________
14. Demuestre que las tres medianas de un triángulo son concurrentes y que el punto de concurrencia, el centro de gravedad, es de dos tercios de la distancia de cada vértice al lado opuesto.
¿Cómo utilizaría SPG para ayudar a los estudiantes comprender esta relación del triángulo y sus puntos medios? ¿Cómo desarrollar un sentido de la prueba de la relación con los estudiantes?
________________________________________
15. Demuestre que las tres bisectrices de los ángulos internos de un triángulo son concurrentes.
________________________________________
16. Demostrar que cualquier bisectriz del ángulo de un triángulo es concurrente con las dos bisectrices exteriores de los ángulos opuestos de un triángulo.
Suscribirse a:
Entradas (Atom)